本博客探讨了金融中的预期价值，解释了其在预测结果中的用途、预期价值与风险回报之间的差异，提供了正/负预期价值的例子，以及在交易中提高预期价值的技巧，包括风险管理和回溯测试。
介绍
因此，Twitter 上一位名叫CryptoCred的著名匿名人士发了一条推文，让 Lil Goose 开始思考为什么人们仍然无法区分RR 和 EV，也无法从 EV 或预期值的角度理解事物。在本文中，Lil goose 将介绍什么是 EV，以及如何针对您的交易策略改进它。
什么是 EV？
期望值是概率论中的一个重要思想，在经济学、金融学和统计学中有着广泛的应用。
它代表了人们从特定事件中可以预期的平均结果。这一概念使我们能够预测特定情况的预期结果，这有助于做出明智的选择，即交易
简单来说，EV 是某个事件的每个结果的提交乘以该结果发生的概率。
你可以将其视为频率（X 发生的概率）* 幅度（结果）
它和 RR 有何不同？
预期价值和风险回报是金融和经济学中用于评估潜在结果的两个不同概念。预期价值表示某人从给定的一组结果或事件中可以预期的平均结果。同时，风险回报衡量特定投资或决策的潜在回报与相关风险。
因此，下次您看到有人发布20 RR 交易（即回报是风险的 20 倍）时，不要大吃一惊，因为他们的 EV 仍然可能是负的。
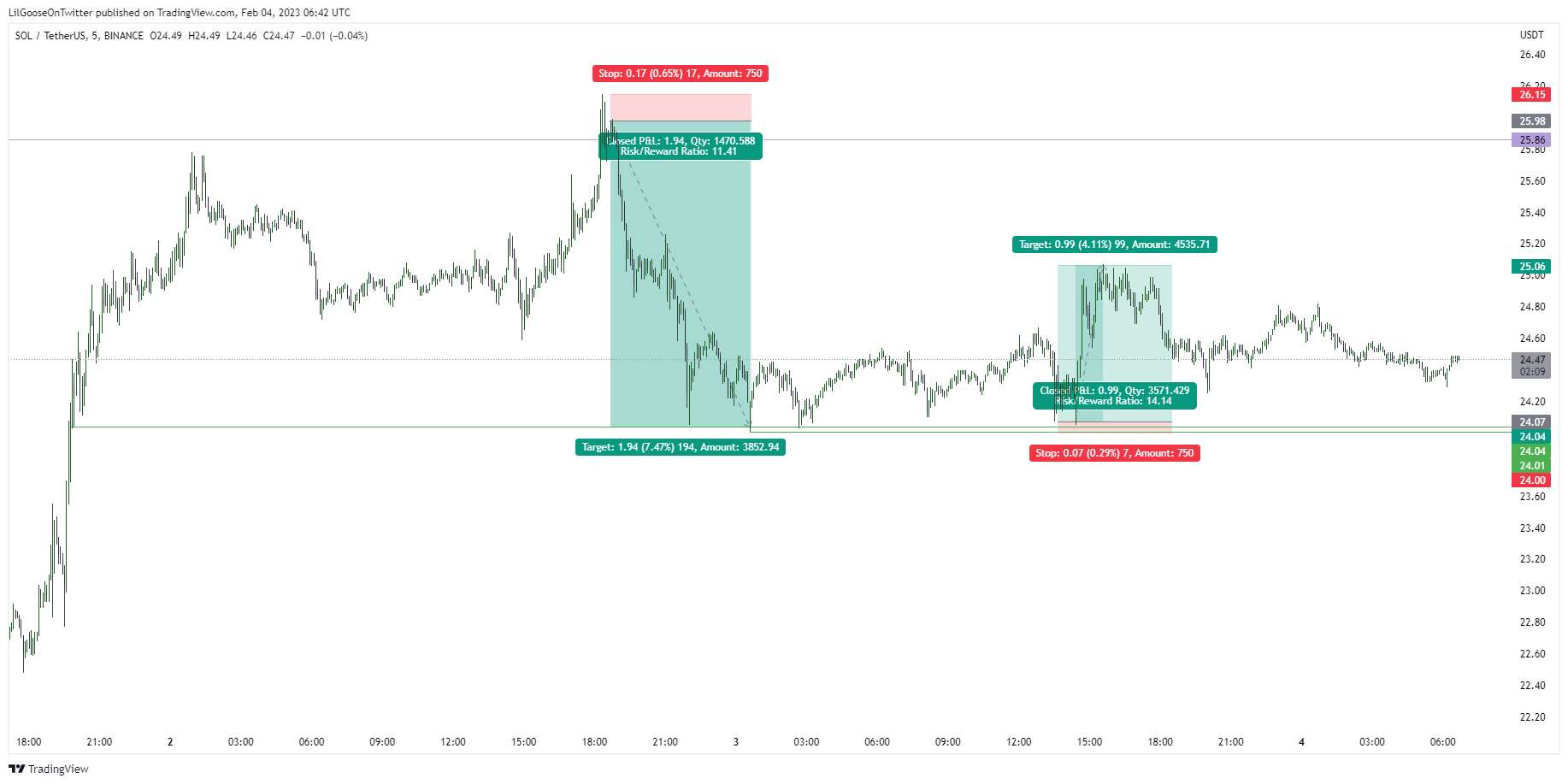
现在，我们知道了 EV 是什么，那么正 EV、负 EV 甚至零 EV 又意味着什么呢？
正 EV 表示在无限期内，平均结果预计为盈利，而负 EV 则表示平均结果预计为亏损。最后，零 EV 只是表示您的系统在无限期内既不盈利也不亏损。
让我们通过几个基本的例子来更好地理解这一点！
示例
现在我们先举一个骰子的基本例子。如果骰子落在任意数字 X 上，您就会得到 $X；也就是说，如果骰子落在 4 上，您就会得到 $4！
我们知道骰子任意一面的概率都是⅙；因此，EV 或预期值将是：
（⅙*1）+（⅙*2）+（⅙*3）+（⅙*4）+（⅙*5）+（⅙*6）= 7/2 或 3.5
这意味着如果您无限次掷骰子，每次掷骰子您平均会得到 3.5 美元。
现在，让我们再稍微有趣一点，假设你掷出 6，你就输 6 美元！
因此，您得到六的结果是-6 美元而不是 6 美元，所以 EV 方程现在变成：
（⅙*1）+（⅙*2）+（⅙*3）+（⅙*4）+（⅙*5）+（⅙*（-6））= 3/2 或 1.5 美元
因此您会发现 EV 现在已经发生了巨大的变化！
解决了这些问题后，让我们将同样的方法应用到交易系统中。在这种情况下，我们只有两种主要结果。要么赢，要么输。
因此，假设您的策略胜率为 70%，您冒着损失20 美元的风险，而这笔交易的回报为50 美元。
因此，该交易的期望值为：
（0.7 50）+（0.3（-20））= 29美元，
这意味着如果您交易该策略，您将在无限期内平均每笔交易赚取 29 美元。
您也可以以 RR 的形式计算。对于相同情况，我们的 RR 为 50/20 = 2.5。因此，如果您赢了，您将获得 2.5 RR；如果您输了，您将损失 1RR。
因此，期望值为：
（0.7 2.5）+（0.3（-1））= 1.45 RR。
因为 1R = 20 美元，所以 1.45RR 就是 = 1.45*20 = 29 美元！
这是一个简单的备忘单，可帮助您查看您的盈亏平衡胜率，如果您的策略的 WR 大于该胜率，则意味着您的策略为 +EV！
提高交易系统估值的方法
有多种方法可以提高系统的 EV。
风险管理：通过止损订单和头寸调整来管理风险可以帮助最大限度地减少亏损交易对预期价值的负面影响。
幸运的进入和可能的退出：著名红辣椒SalsaTekila的一句话是提高您的 EV 的最佳方法之一，但并非最简单的方法。
回溯测试：定期回溯测试交易策略可以帮助确定需要改进的领域并相应地向系统添加新的条件。
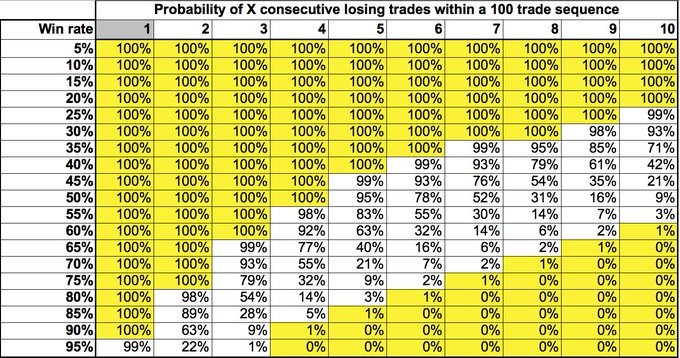在特定赢率下连续亏损 X 次的概率
持续学习：就像回溯测试随着时间的推移会产生更好的 EV 一样，学习新事物和新概念也可以帮助您最大限度地减少损失并最大限度地提高收益，从而提高 EV。
结论
期望值或 EV 是概率论中的一个基本概念，在金融、经济和统计学中有着广泛的应用。它表示某人可以从一组事件或结果中预期的平均结果，其中 EV 为正，这意味着平均结果预计在无限期内盈利，而 EV 为负则意味着平均结果预计会导致亏损。
这一概念对于理解和改进您的交易系统和策略至关重要。有几种方法可以提高系统的 EV，包括但不限于有效的风险管理、幸运的进入和可能的退出以及定期对交易策略进行回测。目标是最大限度地发挥获胜交易的积极影响，并最大限度地减少亏损交易对整体预期价值的负面影响。
